オーダリング手法の違いがもたらすメモリ使用量への影響
数値シミュレーションの業務では1970-1980年代に開発されたフォートランのプログラムが今でも活用されています。古いコードは、長年にわたる実績があり信頼性が高い一方、実行時間が長い、メモリ消費が大きいといった様々な問題があり、大規模問題には適用できないものも見受けられます。
その原因の一つは、連立一次方程式を解く直接法にあります。当時の直接法のサブルーチンは密行列や、スカイライン法等の簡単な手法によりオーダリングされた帯行列向けに開発されているもの主流でした。三次元の問題においては、N元の連立一次方程式に対して密行列ソルバではO(N2)、スカイライン法でもO(N5/3)のメモリが必要となります。
しかし、80~90年代に、Minimum degree (MD)およびNested Dissection (ND)の組合せに属する新しいオーダリングの手法が開発さました。これを採用することで、メモリ使用量をO(N4/3)まで低減することができます。
三次元の立方体格子で離散化された方程式について、各手法で必要となるメモリ使用量のグラフは図1のようになります。
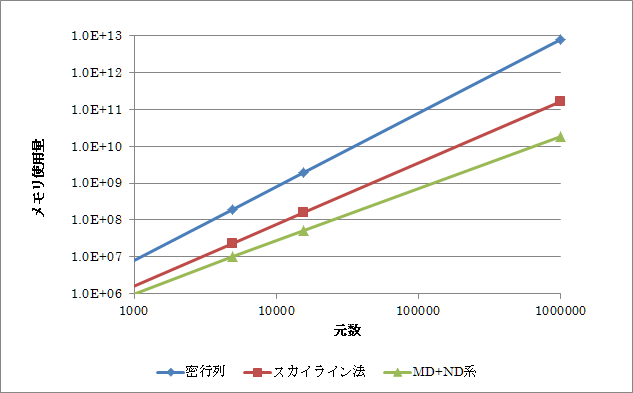
図1 オーダリング手法の違いによるメモリ使用量の理論評価
100万元規模の連立一次方程式では、NDやMDに基づくオーダリング手法では、スカイライン法と比べて1/10、密行列との比較では、1/500という少ないメモリ量で計算が行なえます。
また、これらのメモリ使用量の差は、計算対象となる非ゼロ要素数の差によるものですので、オーダリング手法を変えることで演算時間も大幅に短くすることができます。
実際に、スカイライン法と最適なオーダリング手法の違いを見るために、17×17×17 (= 4913元)の小さい立方体の構造格子で離散化した連立一次方程式について両方のオーダリングを行なった後のメモリ使用パターンを図2、図3に示します。これらの図で黒い部分は連立一次方程式を解くために記憶する必要のある領域で、白の部分は不要な領域です。
スカイライン法が使用しているメモリの領域はきれいな帯行列となっていますが、2.84e+6個の実数を使用しています。一方、最適なオーダリングにおけるメモリの領域は複雑に見えるフラクタル的な画像となっていますが、スカイライン法の半分以下の1.25e+6個の数しか使用していません。
図 1の理論評価で見たように、方程式数が増大するに連れ、両手法における使用メモリ量の差は拡大します。同様の問題を、100万元(=100x100x100)程度の三次元の格子で離散化した連立一次方程式を解くのに必要なメモリ量は、スカイライン法では、200GBとなり大規模メモリを搭載した特殊な計算機の導入や、スーパーコンピュータ上での分散並列化といったハードもしくはソフト面での追加投資が必要になります。
一方、最適なオーダリング手法を用いでば、同じ問題に対して必要なメモリ量は20GB前後に抑えられ、一般的なワークステーションでも計算可能となります。

図2 スカイライン法によるオーダリング後に記憶が必要となる行列の要素

図3 最適なオーダリング手法を適用した時に記憶が必要となる要素